ALEXANDER SHIDLOVSKY [DR. OF PHILOSOPHY] CANDIDATE OF TECHNICAL SCIENCE
THE HYDROGEN ATOM IS THE SIMPLEST OF ATOMS.
( CONTINUATION OF THE THEORY OF NIELS BOHR )
PART 1
INTRODUCTION
The Quantum mechanics theory permits to calculate many points in the micro-physics sphere, but at the same time it is very difficult to
understand natural physics phenomenon.
So, we introduce to you attitudes of some Nobel laureates.
Here it is the Richard Feynman`s
opinion, Nobel laureate for 1965 year:”…it is seem to me, that I can take the
liberty to say, that nobody could understand the Quantum mechanics…If you can
not be suffered from the question: “How
it can be though? On the contrary matter, you will fall in deadlock, from which nobody still had way away”. 1]
"When new ideas came in, I would try
either to deduce them, if they were deducible or to explain that it was a new
idea ... and which was not supposed to be provable." The Feynman Lectures
on Physics
Nobel laureate for 1969 year Murrey Gell-Mann:” The Quantum mechanics is a discipline full of puzzles and paradoxes, which we don`t understand
for the end, but we can use it,... and
as sociologists will say this is the unintuitive discipline”.2]
Nobel laureate for 1979 year, Abdus Salam: “ Included ourselves in limits of the Quantum mechanics we had built the house without doors and windows
and with so high walls, that we could not understand yet, where we are in the house or in the prison”.3]
Nobel laureate for 1979 year, Steven Veinberg about the Quantum
mechanics: “But I admitted, that I sense some discomfort, when all the life I had used the
theory, which nobody understands clearly “. 4]
What is the cause of such difficulties in the
understanding even for Nobel laureates in physics?
The Noble laureate for 1933 year Paul
Adrien Maurice Dirac being one of
the Quantum mechanics creators, included his 50-years work in
the Quantum theory in such way: “
….It seems to me rather probably that some time in the future
it will appear improved Quantum
mechanics, in which will be returning
to causation… But such causation
approach may be possible, only, as a cost of the refusal from any another fundamental idea, which
now we unconditionally assume. “[B.5]
So, many difficulties of the Quantum mechanics
understanding may be caused by an imperfection, for example, this is an absence
of the causation.
In accordance to Paul Dirac, it could be returning for causation in future and as result to the more physical
clearness.
The Quantum mechanics is not every time adequate
instrument describing microcosm of the lack causation, mathematical complication and abstraction.
Therefore, it is need to found another “instruments”
of supplemented possibilities for Quantum mechanics.
1. Richard Feynman. «The character of physics laws».
2. «Fundamental structure of substance». Collection of articles. Translation from English, M: MIR, 1984, p. 266
3. Abdus Salam. Progress ( success) in the physician science, 1969. v99. B.4, p573.
4. Steven Veinberg. The dreams about final theory. M., LKI, 2007.p.69.
5. Paul Dirac . Ways in physics». M, Energyatomizdat, 1983. p.15-16.
THE BASE PART
In our work as a more actual direction of the hydrogen atom theory,we took the process of electron irradiation between stationary orbits, and it have been examined on the base of classical physics.
The author shows us three fragments. They are from his several books united by one title: The hydrogen atom is the simplest of atoms.
Author examined the electron conversion, using two assumptions – postulates, based on classical physics apparatus:
1.The electron conversion occurs, according to mechanics, on decreasing spiral orbits.
2.During the conversion, electrons are losing part of energy, according to electrodynamics, through emitting irradiation photon.
THE FIRST BOOK
ELECTRON IRRADIATION TRANSITION IN THE HYDROGEN ATOM OF THE BOHR MODEL
1.1. Losses of energy in transition
1.2. Losses of the momentum quantity
1.3. The time of electron transition
1.1. LOSSES OF ENERGY IN TRANSITION
Here we will examine irradiation electron transition between adjacent stationary circular orbits in the Hydrogen atom.
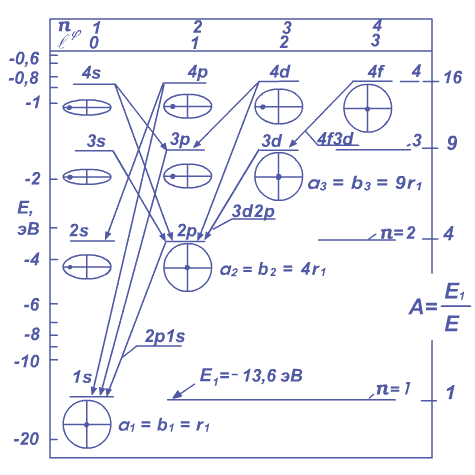
During such transition, the electron movement is occurring at circular decreasing spiral orbits about the atomic nucleus.[1.1.1] These are conversions 2p1s, 3d2p, 4f3d, ...etc. They are showed on the figure 1.1.1, where on the left ordinate axis is the electron energy E in electron-volt (eV). On the right ordinate axis is put relative data of station energy:
a – electron charge
is an radius of n- number stationary circular orbit of
electron
is the
electron energy, at first stationary circular orbit with radius 
.
When an electron conversed at (n –1)- stationary circular orbit, more close to atomic nucleus, this electron will have energy:
Fig. 1.1.1. This is simplified scheme of energetic levels and irradiation electron transition conversions in the hydrogen atom.
There at the top abscissa are putted meanings of the azimuth quantum number 
Zommerfield and the orbital quantum number 
Lande ,
elliptical and circular
orbits of an electron showed illustrated, nucleus is alike spot. Large half-axes elliptical orbits conditionally are given of one size.
The loss of energy in such transition will be
In this expression (1.1-4) the law of conversation of the energy is registrated the loss in an electron. However, the conformity of this process of losing energy doesn`t reflected.
The transition is showed as an electron jump from the n to ( n – l ) energy state.
Let us examine the question of losing energy by electron in transition between neighbouring stationarycircular orbits. At the beginning, when an electron spontaneously leaves the stationarycircular orbit, it lays under the electrodynamics law. In particular, the circulation of the electro- charged electron on a circular orbit is the curvilinear movement with acceleration, and because of that an electron has to lose it energy through the emission of electromagnetic irradiation.
Losing the energy, electron moves on spiral reducing circle about hydrogenatom nucleus.The losses of an electron energy is connected with the changing of the spiral circle radius correlation
This relation had been received from the differentiation of the expression (1.1–2) to the current meaning of the electron energy E.
During the transition time, from the stationary circular orbit with the
radius 
to the near by (n – 1) stationary circular orbit with the
radius 
, the electron is losing it energy, and photon carries it away.
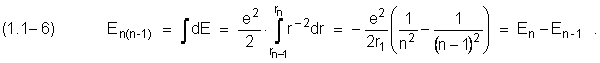
Energy amount, lost by electron in that transition process, coincides with the expression (1.1–4), had been received by using the law of conservation energy. Now, the electron transition between stationary circular orbits is seemed as a process of gradually loss energy, but not as ‘jumping’ between energetic levels.
The electron movement in such transition is determined by laws of
conservation energy, mechanics and Coulomb's law. And so, in the absence of the
external influence on the electron movement by circular and spiral orbits the element of happening could not be.
1.1.1) Shidlovsky A. The Hydrogen atom is the simplest of atoms. MINSK: VAVAR, 1997.p.57-61
1.2 LOSSES OF THE MOMENTUM QUANTITY
We`ll examine the process of gradually loss energy by M electron at the transition, between the near by stationary circular orbits. It should be noted, that Quantum mechanics considers this only from the point of the moment conversation law, but not examines the process of losing orbital moment by an electron during the transition.
v, r - current meanings of electron speed and orbit radius,
m – an electron mass.
We use, for the case of the current circular orbit of the electron, the famous formula of the hydrogen atom of Bohr theory [1.2.1]:
Let us put the expression (1.2–2) for the electron speed v in (1.2–1):
After differentation of (1.2-3) it is received the dependence of the electron moment loss dM from reducing of the radius to dr:
During the electron transition process from the stationary circular orbit of the radius to the near by stationary circular orbit with the radius , electron loses and photon take away quantity of motion moment :
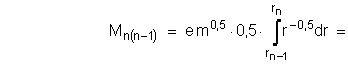
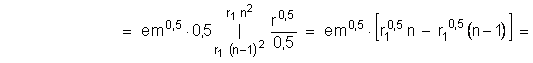
For the simplification of (1.2-5), we used expression (1.2-2) for
the first stationary state of the hydrogen atom, where electron speed and radius of it orbit
is 
and 
, so it had been used the Bohr theory
expression[1.2.1]:
Therefore the moment of motion quantity, gradually lost by electron in transition and the moment taken away by photon turns out to be equal to the Plank constant ħ, that in accordance with the result received when we using law of the moment of motion. Now, we can see gradual quantity loss of motion moment, according to reducing of electron radius orbit during the electron transition.
The importance of this result is, that the Plank constant ħ, according to (1.2.- 5), reformed in visible physician sence or meaning. It is eqaul to integral ( sum ) of current quantity of motion moment losses, in the electron transition process between the near by stationary circular orbits.
1.2.1) Shidlovsky A. The Hydrogen atom is the simplest of atoms. MINSK: VAVAR, 1997.p 16.1.3. THE TIME OF ELECTRON TRANSITION
In the Quantum theory Bohr says: “…There is not at all examined the time, during which transitions are happening”[1.3.1], and “…the question about time interval, during which the connected to transition irradiation is happening, arises many difficulties. “[1.3.2]
Let us define the transition time of electron between near by stationary circular orbits, on the base of classical physics.
An intensity energy of irradiation, according electrodynamics, is written like current energy velocity of losses by electron, during the transition process between near by stationary circular orbits
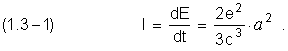
C - it is the light velocity
Then,
we can obtain expression for electron
acceleration at the current orbit, using
(1.2–2):
We can found the correlation 
, using (1.1–5):
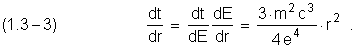
Integrating (1.3–3)
and using (1.2–2), it is defined electron transition time between near by stationary circular orbits; at
the same time , .
Here 
it
is a constant of subtle slim structure
The turning interval of electron at the first, stationary circular orbit is:
(seconds) [1.3.3].
Relative meaning of the large half-axis of this orbit
Relative electron rotation number at the first stationary circular orbit, with the losses of energy 
with intensity 
[1.3.4] :
(rotations).
Relative time of the electron energy losses with
intensity 
time
at the first stationary circular orbit is:
(seconds)
For this case, the meaning for spiral circular orbit electron transition of the large half-axis of the orbit is:
Relative meaning of the electron orbit radius R is:
In the table 1.3.1. is compared electron transition time 
, calculated in this work, with
the transition life time 
from Quantum mechanics data. The first line, in the table 1.3.1., reflects formally «1sp»
electron transition from the first the first stationary circular orbit, where n =1,
to the – proton, where 
.
Another five transitions satisfy to the first lines of the Balmer, Paschen, Brackett, Pfund ….series. In the second column of the table 1.3.1. is given probability W of electron transition from Quantum mechanics data. [1.3.5].
In the third column there is cited the transition life time:
In the forth column there is cited approximated meanings of the life time calculated by (1.3 – 4) .
Table 1.3.1.
Transition |
Transition approximation
|
Life time of Transition
|
Time of Transition by (1.3-4)
|
Time ratio
|
1 |
2 |
3 |
4 |
5 |
«1sp» 2p1s 3d2p 4 f 3d 5g4 f 6h5g |
– 6,26 · 10 8 6,46 · 10 7 1,38 · 10 7 4,25 · 10 6 1,64 · 10 6 |
– 0,16 · 10 – 8 1,55 · 10 – 8 7,25 · 10 – 8 23,5 · 10 – 8 61,0 · 10 – 8 |
1,55 · 10 –11 0,98 · 10 – 9 1,04 · 10 – 8 5,24 · 10 – 8 18,0 · 10 – 8 48,3 · 10 – 8 |
– 1,63 1,49 1,38 1,31 1,26 |
As
it seemed from fifth column in the table 1.3.1., that
the difference between life time 
and transition time 
of electron is comparably not great, but it has a systematic monotonous character,
reducing with the increasing of
transition number.
As
it seemed from fifth column in the table 1.3.1., that
the difference between life time and transition time of electron is comparably not great, but it has a systematic monotonous character,
reducing with the increasing of
transition number.
Now we want to note the following. Comparative values in the table 1.3.1 
and have different physical meaning.
In Quantum mechanics irradiation life time
is determined, as a time during which the
quantity of excited state atoms
reduced in 2,72 times.
Itis in this work electron transition time between stationary states (stationary circular orbits).Though an electron during the time non-stop emits energy.
is equal to photon emission time 
.
A photon can be showed with the wave organization.
For example, in the case of 3d2p transition, time duration of photon, according the table 1.3.1., is
And its linear extent is
С – light velocity .
1.3.1 N. Bohr. « Selected scientific transactions».O. 2. I.: Science, 1971, p. 24
1.3.2 N. Bohr. «Selected scientific transactions».O. 1. I.: Science, 197,. p. 530.
1.3.3 Shidlovsky A. «The Hydrogen atom is the simplest of atoms» MINSK: VAVAR, 1997.p. 32..
1.3.4. Shidlovsky A. «The Hydrogen atom is the simplest of atoms». MINSK: VAVAR, 1997.p10
1.3.5 Sobelman I.I. «Introduction to theory of atomic spectrum» I.: Science, 1977. p. 295.
1.4. GENERAL RESULTS
We present, in short, other results, obtained in the work at definition characters of irradiation electron transition in the hydrogen atom of Bohr model:
it is showed, that the electron emits energy with intensity required by electrodynamics; the quantity of electron revolution around the nucleus is determined.
Results of expressions (1.1–6) e (1.2–5) confirm in particular our supposition about circular character of the electron motion at spiral reducing orbits in examined transitions of the hydrogen atom.
So, on the base of classical physics, problems for the hydrogen atom, which still are impossible to be raised in Quantum mechanics, are solved.
In our case, we used obvious model of the electron motion and applied simple mathematics.
This material is given in the book: Shidlovsky A. "The Hydrogen atom is the simplest of atoms. The continuation of the Nilce Bohr theory." MINSK: VAVAR, 1997.p
The author with gratitude accepts remarks and suggestions.
Full information is available at http://atom-of-hydrogen.narod.ru (in Russian only).